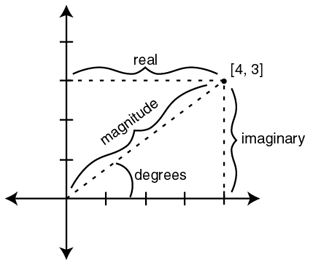
The sum_of_squares attribute is simply the magnitude attribute without taking the square root. For the point [4, 3] shown in the diagram the values of magnitude and sum_of_squares are as follows:
There are six available attributes for any complex number:
Below is a diagram showing the complex number [4, 3]. The attribute values for real, imaginary, magnitude and degrees are labeled for that point.
| attribute | formula | value |
|---|---|---|
| magnitude | sqrt(4 * 4 + 3 * 3) | 5 |
| sum_of_squares | 4 * 4 + 3 * 3 | 25 |
The reason for having both sum_of_squares and magnitude is that since the magnitude calculation involves taking a square root it is slower than the sum_of_squares calculation. It is often possible to create an equivalent (but more quickly generated) fractal image by using sum_of_squares instead of magnitude
| attribute | short form | examples |
|---|---|---|
| real | real | real(z), real([1, 2]) |
| imaginary | imag | imaginary(z), imag([2, 3]) |
| magnitude | mag | magnitude(z), mag([3, 4]) |
| sum_of_squares | ssq | sum_of_squares(z), ssq([4, 5]) |
| degrees | deg | degrees(z), deg([5, 6]) |
| radians | rad | radians(z), rad([6, 7]) |