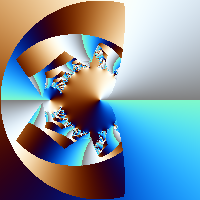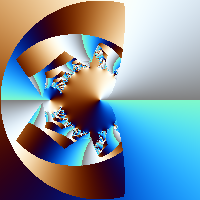Regions

All Fract-O-Rama formula files have a section that looks like this: 

  formula
  {
     zero or more statements

     while(some_condition)
     {
        zero or more statements
     }

     zero or more statements
  }

The 'while(some_condition)' part specifies the conditions under which the program will continue to execute the statements inside the while loop.

Here is a complete formula file with a typical while loop condition: 

  fractal
  {
     mapping { (-2, -2, 2, 2) => (200, 200) }

     formula
     {
        z = [0, 0];

        while($count < 20 && ssq(z) < 4)
        {
           z = z ^ 2 + current;
        }

        $value = deg(z) * (255 / 360.0);

        set_color($value, $value, $value);
     }
  }

Many interesting fractals can be generated by varying the condition that governs the while loop. Regions are one such mechanism, they provide a way to test to see if a point is within a certain area. Typically this is used in a manner like this: 

  fractal
  {
     mapping { (-2, -2, 2, 2) => (200, 200) }

     formula
     {
        z = [0, 0];

        while($count < 20 && ssq(z) < 4)
        {
           if(inside(z, /* some region */))
           {
              // our 'z' point is inside the region, leave the
              // while loop prematurely

              break;
           }
           z = z ^ 2 + current;
        }

        $value = deg(z) * (255 / 360.0);

        set_color($value, $value, $value);
     }
  }
Above /* some region */ is a placeholder for an actual region but we can see how we go about testing to see if a point is within a region and now we'll look at the different types of regions that are available.

There are 6 types of regions and 4 ways to combine regions. First, we'll look at the region types.

Region Explanation 
r_circle(center, $radius)
 This region describes a circle centered at 'center' with radius '$radius' 
r_cross(p1, p2, $barWidth, $barHeight)
 This region describes a rectangular area (p1 and p2 are the corners). The cross is incribed within the rectangular region and the thickness of the horizontal bar is '$barHeight' the thickness of the vertical bar is '$barWidth' 
r_ellipse(center, $xradius, $yradius)
 This region describes an ellipse whose center is 'center'. The width of the ellipse is governed by '$xradius' its height by '$yradius' 
r_poly(p1, p2, ..., pN)
 This region is a polygon defined by the points p1, p2, ..., pN. There must be at least 3 points but there is limit on the maximum number of points 
r_spoly(center, $nSides, $radius, $angle)
 This region describes an '$nSides'-sided polygon whose center is 'center'. The value '$radius' indicates the distance from the center to any of the polygon's '$nSides' points. The '$angle' value rotates the polygon around its center, if this value is zero one point of the polygon will be at 0 degrees (3 o'clock). 
r_rect(p1, p2)
 This region describes a rectangle whose opposite corners are the points 'p1' and 'p2'

Now let's look at some images of what these regions actually look like. For this discussion we'll assume the following: 


r_circle([.5, 5.], .4)
 

r_circle([.4, 4.], .2)
 

r_cross([.2, .2], [.8, .8], .2, .4)
 

r_cross([.1, .1], [.9, .9], .3, .1)
 

r_ellipse([.5, .5], .4, .2)
 

r_ellipse([.5, .5], .2, .4)
 
r_poly([.2, 0], [.3, .3], [.2, .3], [.3, .6],
       [.2, .6], [.4, 1],  [.3, .7],[.4, .7],
       [.3, .4],[.4, .4], [.2, 0])
 

r_poly([.1, .1], [.2, .8], [.9, .3])
 

r_spoly([.5, .5], 5, .4, 0)
 

r_spoly([.5, .5], 6, .4, 20)
 

r_rect([.1, .1], [.7, .8])
 

r_rect([.3, .4], [.9, .1])

Now lets look at the mechanisms for combining regions

r_and(region1, region2) Specifies the area that is in both region1 and region2
r_or(region1, region2) Specifies the area that is in either region1 or region2
r_xor(region1, region2) Specifies the area that is in either region1 or region2 but not both
r_not(region) Specifies the area that is not in region

For these examples, we'll be using the following regions/images: 


region1: r_circle([.3, 5.], .25)
 

region2: r_circle([.6, 5.], .25)

Here are images showing the different mechanisms for combining regions 


r_and(region1, region2)
 

r_or(region1, region2)
 

r_xor(region1, region2)
 

r_not(region1)

Finally, it is worth noting that the combining mechanisms (r_and, r_or, r_xor, r_not) are regions themselves so they can also be combined. Here are some examples: 


r_not(r_xor(region1, region2))
 

r_not(r_or(region1, region2))

And here is a complete formula file that uses regions and the image it produces 

   fractal
   {
     mapping {
      (-2.00000000000000000000,
       -2.00000000000000000000,
       2.00000000000000000000,
       2.00000000000000000000) => (200, 200)
     }
 
     formula
     {
        z  = [0, 0];
        p  = [1, 0];
        $n = 3;
        $r = 2.0;
        $a = 0.0;
 
        while($count < 20 && ssq(z) < 4)
        {
           z = z ^ 2 + current;

           z1 = asech(z);
           z2 = conj(z1);

           if(
              inside(z1, r_spoly(p, $n, $r, $a)) ||
              inside(z2, r_spoly(p, $n, $r, $a))
           )
           {
              break;
           }

        }

        $r = $g = $b = 0;
 
        $value = deg(z) / 360.0 * 2.0 * $m_pi;

        $r     = 127.5 + 127.5 * sin(1.0 * $value);
        $g     = 127.5 + 127.5 * sin(1.2 * $value);
        $b     = 127.5 + 127.5 * sin(1.4 * $value);
 
        set_color($r, $g, $b);
     }
  }